Creating Artificial Data with Gaussian Noise
A quick look at adding simple Gaussian noise to existing data to create artificial samples, and how it can sometimes boost performance.
ARTIFICIAL / SYNTHETIC DATA
8/4/20254 min read
There are many potential use cases for artificial data — from testing model robustness, to simulating rare events, to augmenting small datasets.
In this post, we’ll focus on one straightforward approach: adding Gaussian random noise to existing data. It’s not a sophisticated method — the noise is, after all, random — but it’s quick to try and can, in some cases, surprisingly boost model performance.
In upcoming posts, I’ll explore other techniques for generating artificial data and how they can be applied in different contexts. But for now, let’s look more closely at what I mean by “boost model performance” in this context.
How to check if the noise improves model performance
When I say “boost model performance”, I’m talking about improvements seen in simple experiments, such as for instance:
Split your data into train and test sets.
Create noisy, artificial points from the training set (or a subset of it).
Train your model on the combined original + noisy training data.
Evaluate performance on the test set.
If your model performs better on the test set — and does so consistently across multiple random seeds — then adding Gaussian noise has helped.
In other words, the noisy data has acted as a form of data augmentation that improved generalization.
Variants and tweaks worth exploring
While the basic idea is to add Gaussian noise to your data, there are plenty of ways to adapt and extend it. For example:
Use a targeted subset of the training data when generating synthetic points — for instance, oversample rare but important patterns that you want the model to see more often.
Vary the noise level by feature, adjusting based on each feature’s scale, importance, or robustness to perturbation.
Augment the test set by adding noise and making predictions on this artificial version as well.
A variation I’ve seen work in some cases is to turn this into a two‑model ensemble:
Train a model on the original training data and predict on the original test data.
Train a second model on the synthetic training data and predict on the synthetic test data.
Ensemble the predictions from both models.
This can sometimes improve stability and accuracy, as the two models may capture different aspects of the problem.
Adding Gaussian noise — a simple implementation
We’ve looked at a few different ways you could adapt and extend the basic idea of adding Gaussian noise. Now, let’s move from concepts to code and see what a simple Gaussian noise function might look like in practice.
Below is a minimal Python function that adds Gaussian noise to selected features in a DataFrame:
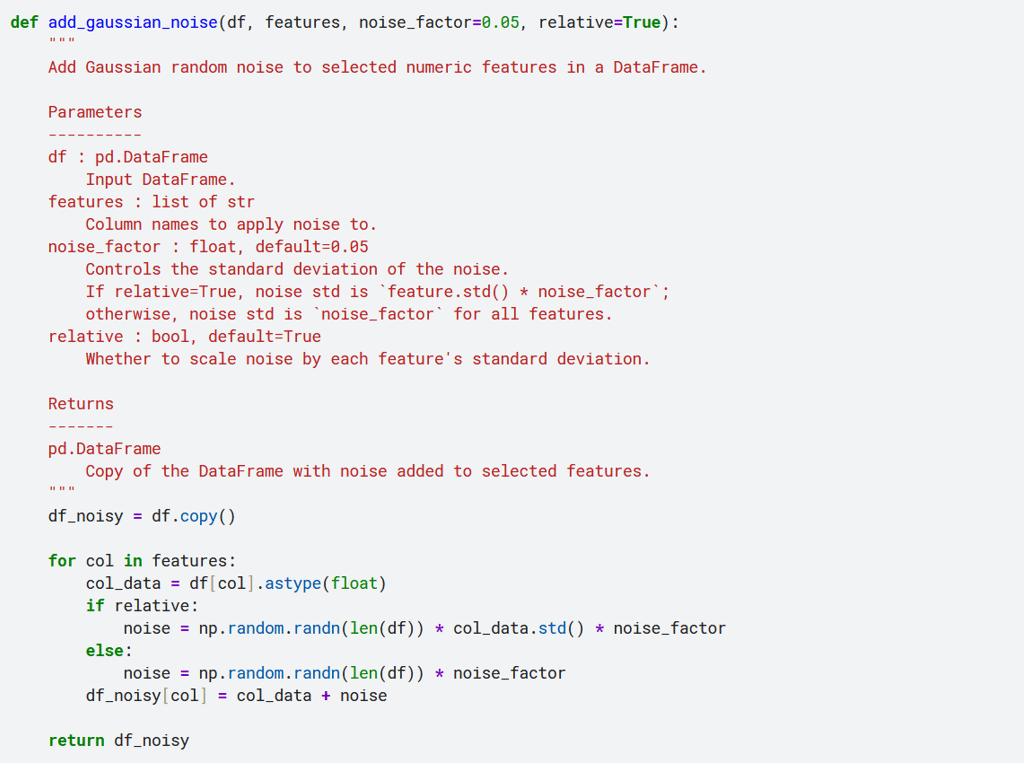
As shown in the image above, the function allows you to control the amount of Gaussian random noise added to the data by adjusting the noise_factor parameter.
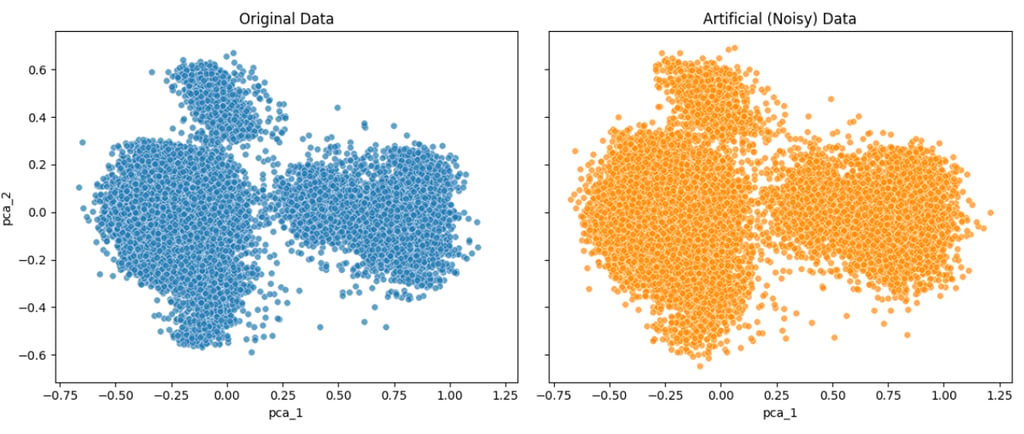
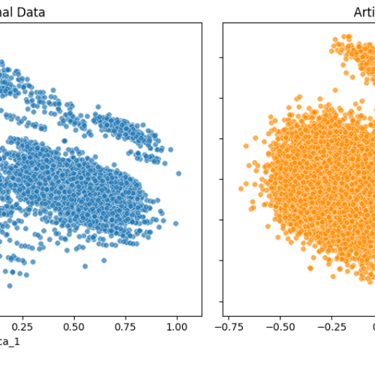
Below are two examples from a Kaggle dataset—one with a lower noise factor (noise_factor = 0.5) and one with a higher noise factor (noise_factor = 2.0).
For visualization, I applied PCA to reduce the dataset to two dimensions and plotted the results. In addition, I measured how strongly column A in the noisy dataset correlates with its counterpart in the original dataset for both noise levels.
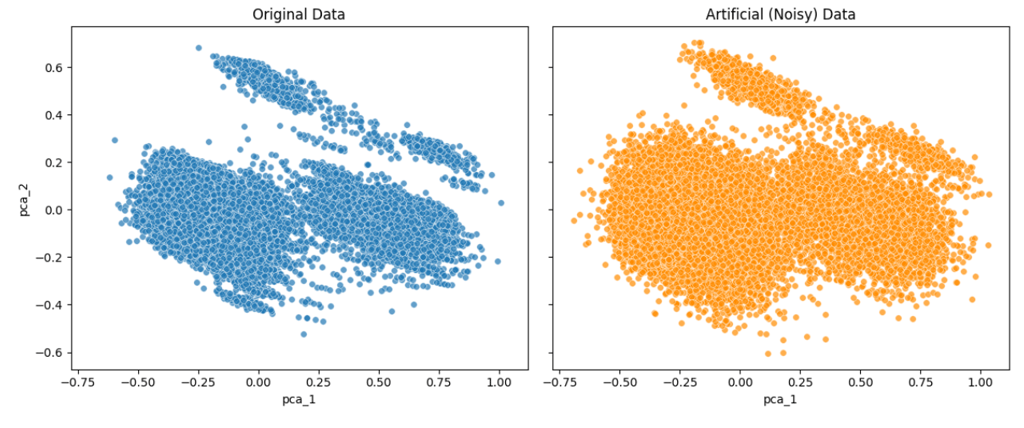


Noise factor = 0.5:
Noise factor = 2.0:

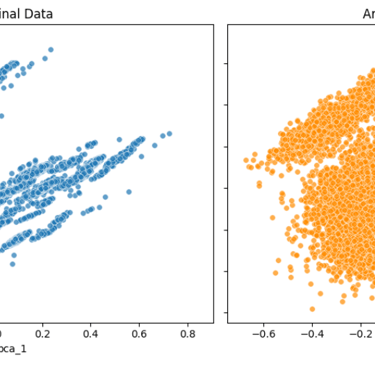
As shown by both the PCA plots and the correlation values, increasing the noise factor makes the artificial data progressively less similar to the original data.
Finally, we compare the average AUC over 25 random seeds for a model trained on the original training data versus one trained on the same data augmented with noisy samples generated at multiple noise factors.




As can be seen in this case, augmenting the original data with noisy samples resulted in a model that achieved only a slightly higher average AUC than training on the original data alone.
In summary
We showed a simple way to add Gaussian noise to create artificial training data and found that it can, in some cases, be an effective data augmentation technique. However, it’s not a silver bullet — sometimes it works really well, sometimes only marginally, and sometimes not at all. That said, its simplicity and speed of implementation makes it well worth trying.