Gradient Boosting from Scratch — With Residual Dropout and Linear Models in Leaves

With libraries like LightGBM, CatBoost, and XGBoost available, it might seem unnecessary to build your own gradient boosting model. But doing so is a fun exercise: it’s simpler than you might expect, it lets you experiment with new ideas, and most importantly it deepens your intuition about how boosting works.

In this article, we won’t reinvent decision trees from scratch; instead, we’ll rely on scikit-learn’s implementation and focus on building a simple baseline booster. From there, we’ll extend it with custom features like residual dropout and linear regression in the leaves.

Let's start off with a simple baseline model and then build on top of it. The code below should be fairly self-explanatory and includes some comments, so we won’t go through it in detail here.

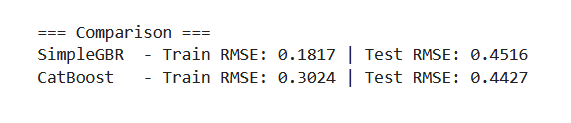
Now, let's test this simple implementation on the famous California housing dataset to see how it compares against CatBoost. This is just a single train–test split, so an optimized CatBoost model will almost certainly perform much better than our baseline.

It’s also worth noting that the parameters in CatBoost are not directly comparable to those in our custom implementation, and CatBoost includes many more defaults out of the box. So this comparison should only be seen as a sanity check to confirm that our implementation works.

The testing code is shown below, followed by the corresponding results.

As expected, the CatBoost model performs slightly better on the test dataset, though our baseline remains competitive. Next, we will enhance the baseline model by introducing additional functionality and experimenting with creative ideas such as fitting linear regression models within the leaves and applying residual dropout.

Residual dropout

Residual dropout is a simple regularization trick we can add to gradient boosting. Instead of letting every tree see the full set of residuals, we randomly mute some of them before training a tree. This introduces stochasticity and prevents the model from overfitting too quickly.

To control this behavior, we add a few parameters to our class:

• dropout_proba (float between 0 and 1)
  The probability that a given residual will be “dropped.” For each sample, we flip a coin: with probability dropout_proba, that sample’s residual is scaled down.

• dropout_weight (float)
  The factor by which a residual is scaled if it is dropped.

  • If dropout_weight = 0.0, dropped residuals are completely removed (true dropout).

  • If 0.0 < dropout_weight < 1.0, dropped residuals are weakened but not eliminated.

  • If dropout_weight = 1.0, dropout has no effect.

• dropout_iteration (int or None)
  The iteration number that defines the cutoff for applying dropout.

  • If None, dropout is never applied.

  • If an integer, it specifies the “nth tree” in the sequence that determines when dropout is active.

• apply_dropout_after (bool)
  Determines whether dropout is applied before or after the specified dropout_iteration.

  • If True, dropout is applied on iterations after dropout_iteration.

  • If False, dropout is applied on iterations before dropout_iteration.

To keep things simple and avoid overloading the implementation with too many features at once, we’ll begin by adding just the residual dropout mechanism. The updated code is shown below:

Once again, let’s test our implementation to make sure it works:

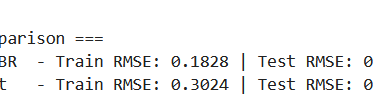
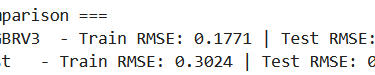
Interestingly, we observe a slight improvement when using residual dropout. That said, this is just a single run with one random seed, so we shouldn’t read too much into it yet.

Linear regression in leaves

Next, we will add linear leaves to our "residual dropout boosting regressor". Normally, each leaf in a regression tree just predicts a constant (the mean of the targets in that region). With linear leaves, each leaf will instead be able to fit a few tiny univariate regressions. We’ll pick the top-k features that vary the most inside the leaf, fit a simple linear model on each, and then average their predictions.

If a leaf doesn’t have enough samples, it will fall back to its mean. To keep things simple at first, we’ll choose the features based on their variance. Later, we may improve this by ranking features with respect to correlation (or similar measures) with the target, which could give better predictive performance.

The implementation of this extension, along with an illustrative example, is provided below.

We observed an improvement for the particular seed shown here when linear leaves were added. Results from other random seeds (not shown) suggest that the linear-leaf variant can sometimes outperform the simpler custom models, though this is not always the case. Since these experiments were run with a limited set of hyperparameters and without exhaustive optimization, the findings should be seen as indicative rather than conclusive.

Moreover, the linear-leaf approach relies on univariate regressions over the highest-variance features in each leaf, which is a rather crude criterion, variance does not necessarily imply predictive usefulness, and the method could likely be made stronger with more principled feature selection or more sophisticated leaf models such as multivariate regressions.

In summary

In this article, we a built simple gradient boosting model from scratch using scikit-learn’s DecisionTreeRegressor. On top of this baseline, we introduced a few twists, such as residual dropout for regularization and linear leaves, where each leaf fits small regressions on its most variable features instead of only predicting a constant.

We have only explored a handful of extensions here, but there is plenty of room to go further. On the more conventional side, one could introduce hyperparameters such as subsampling. On the more experimental side, ideas like reducing tree depth every k iterations or making a leaf’s minimum sample size depend not only on its count but also on the variance of the target could be interesting to try. That said, the chances of such experimental features delivering major improvements are probably low, since if they consistently worked well, they would likely already be part of standard libraries. Still, they can be fun to explore and may yield insights or niche gains in specific settings.